Pseudorandom numbers and white noise generation

02 Jun 2018 in English on C++

One of the first tasks we give to all of our interns as a homework is to generate the additive white Gaussian noise (AWGN) and write it to the binary file. In this post, I’d like to discuss this problem a bit.

Why is the task so simple/far from programming/etc one may ask. In my humble opinion, programming languages can be taught quite fast and interns should present that they are willing to learn and some sort of programming attitude of mind. Any good interview and test task are not as important per se, as a good starting point for the conversation. For example:

1. You get to know a person better. Is she asking questions, willing to learn? Can she admit that she was wrong?
2. Discussions also show the way people think, it’s always great to ask why have you chosen XX approach instead of the YY?

With C++11 we have a great option in the <random> header. It is great, but has got two problems with uniform and normally distributed random values generation:

1. Relatively low performance. Not always a problem, but when you restart your application a lot of times and fill a std::vector with another round of AWGN, a second now and then makes a difference.
2. No C++11 support on our platforms.

The code should be reused as much as possible, therefore some of our libraries migrate from our target platforms (ARM and NeuroMatrix) with no C++11 support to the PC models.

I measure speed with the Google’s benchmark and here is the latest run from my local machine: (the benchmark itself may be found here)

06/02/18 23:31:49
Running G:\Visual Studio\random\make\vs141\x64\Release\benchmark.exe
Run on (4 X 2806 MHz CPU s)
CPU Caches:
  L1 Data 32K (x4)
  L1 Instruction 32K (x4)
  L2 Unified 262K (x4)
  L3 Unified 8388K (x1)

Benchmark	Time	CPU	Iterations
uniform_STL_mt19937_real	67 ns	64 ns	11217877
uniform_STL_lce_real	70 ns	65 ns	11217877
uniform_random_real	4 ns	3 ns	213673844
uniform_STL_mt19937_int	9 ns	9 ns	89743014
uniform_STL_lce_int	16 ns	16 ns	56089384
uniform_random_int	4 ns	3 ns	203961397
normal_STL_mt19937	95 ns	88 ns	7478585
normal_STL_lce	135 ns	131 ns	5608938
normal_random	38 ns	36 ns	18696461

In this benchmark I compare three implementations:

1. Mersenne twister from the STL
2. Linear congruential generator from the STL
3. Custom linear congruential generator and the Box-Muller algorithm, implemented in my library

For the uniform distribution, I test for both real and integer values and only real for the normal distribution. One may see significant speedup comparing to the STL version: ~2.4x to the ~21x for the Mersenne twister and ~3.6x to the ~21x for the Linear congruential generator.

Linear congruential generators have relatively small period comparing to the Mersenne twister, but we’re dealing with digital signal processing and Monte Carlo modelling, where buffers’ sizes rarely exceed 2^32.

Okay, we’ve got a buffer with sampled noise data, with two characteristics: mean value and variance. It can be visualized like this:

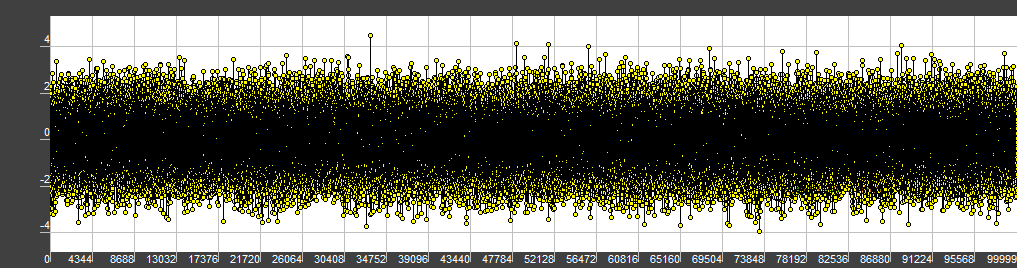
In this article and my job I use our custom digital signal visualization tool, but the easiest way to visualize signal is to use an audio editor, like Audacity. Give it a try!

First of all, we should check the spectrum of this random process, so we can distinguish white, pink, green and other types of noise. Power spectral density of the process may be estimated by the DFT (FFT). Let’s see what we’ve got:

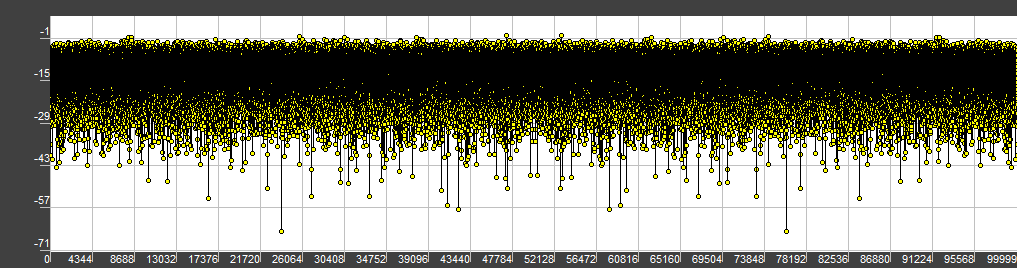
Looks pretty constant to me. Note the logarithmic level axis. Now we have to check the process to be Gaussian. This can be done by calculating the histogram. The histogram represents the probability distribution of some process.

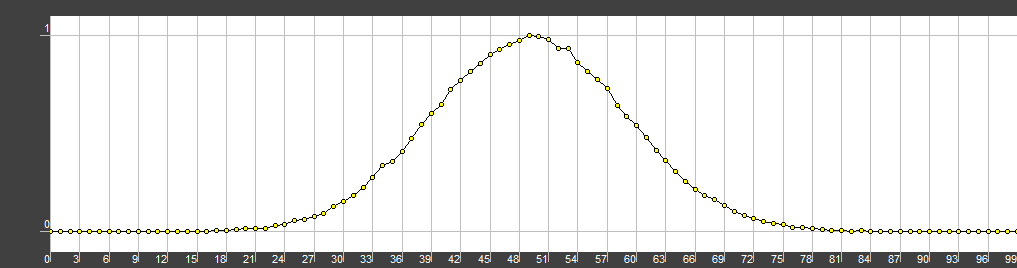
It is always a good idea not only to visually check the histogram but also to recheck the mean and the variance values.

Now we come to the easy part: writing to the file. For the sake of completeness of this article, I’ll discuss this as well, but this is pretty trivial.

void Write(const std::vector<double> &vec, const std::string &filename) {
    std::ofstream of(filename.c_str(), std::ios::binary);
    if(!of.is_open())
        throw std::runtime_error("Unable to open file " + filename);

    of.write(reinterpret_cast<const char*>(vec.data()), vec.size() * sizeof(double));  
}

In this code snippet we try to open the file, check if we succeeded and write the vector data to the file. Voile!

That’s why I love this task. It’s simple, takes no longer than a couple of hours and opens a lot of topics to discuss. I’ve mentioned this earlier in the article, but there’s a library which we use to generate AWGN for our models, which you may find here in case you’re interested.