Constexpr pseudorandom numbers
The last article was more about general stuff and talks, now let’s get to some programming. To make it interesting for the wider audience, we shall try to make everything constexpr. Also, I’ll give you some math and explanations.
The root of all the pseudorandom generators is the so-called “seed”. This is the first number, which will initialize our pseudorandom generators. Since we’re writing compile-time generators, we should also get the compile-time seed. As I’ve mentioned in the last article, for the run-time I prefer to use the std::chrono::high_resolution_clock with its nanosecond resolution. Unfortunately, there’s no such thing in the compile-time, but there is a macro from plain C, which we might want to use: __TIME___.
It will return a const char* string with current time like this: “08:15:59”. First of all, I wanted to use std::from_chars, but it’s impossible due to the lack of the constexpr specifier, so we’ll write our own. Fortunately, we know the format of our input string and we don’t have to worry about all of the corner cases and we get something like this:
constexpr static auto time_from_string(const char* str, int offset) {
return static_cast<std::uint32_t>(str[offset] - '0') * 10 +
static_cast<std::uint32_t>(str[offset + 1] - '0');
}
constexpr static auto get_seed_constexpr() {
auto t = __TIME__;
return time_from_string(t, 0) * 60 * 60 + time_from_string(t, 3) * 60 + time_from_string(t, 6);
}
This seed will reset every day, so if we want to add more randomness, we might want to use the __DATE__ macro, but the current situation is fine for me.
For the uniformely distributed numbers I use the Linear congruential generator. With good parameters (modulus m, multiplier a and increment c) this algorithm provides a long series of non-repeating pseudo-random numbers (up to the \(2^{64}\), as far as I know). It may be formalized this way: \[\begin{aligned} X_n = (a * X_{n - 1} + c) \text{ mod } m \end{aligned}\]
Constexpr functions do not allow variables with extended lifetime (static). This is because constexpr functions should only rely on the underlying algorithms and input parameters, and static variable kinda violates this rule. But, since the linear congruential generator is the state-based algorithm, we have to somehow propagate back the result of the computation. We can make it by passing the value by reference and storing it this way.
constexpr static std::uint32_t uniform_distribution(std::uint32_t &previous) {
previous = ((lce_a * previous + lce_c) % lce_m);
return previous;
}
Getting the array of the uniformly distributed values is pretty simple in C++17 (thanks to the common for loop). In C++11 and C++14 the only way to make a loop was the recursion. Yeah, almost every loop can be converted to the recursion representation, but me personally and many other developers are too lazy for it. Because a user can require an array of any type, first of all, we have to normalize the value, and only then scale and shift it.
constexpr static double uniform_distribution_n(std::uint32_t &previous) {
auto dst = uniform_distribution(previous);
return static_cast<double>(dst) / lce_m;
}
template <typename T, std::size_t sz>
constexpr static auto uniform_distribution(T min, T max) {
std::array<T, sz> dst{};
auto previous = get_seed_constexpr();
for (auto &el : dst)
el = static_cast<T>(uniform_distribution_n(previous) * (max - min) + min);
return dst;
}
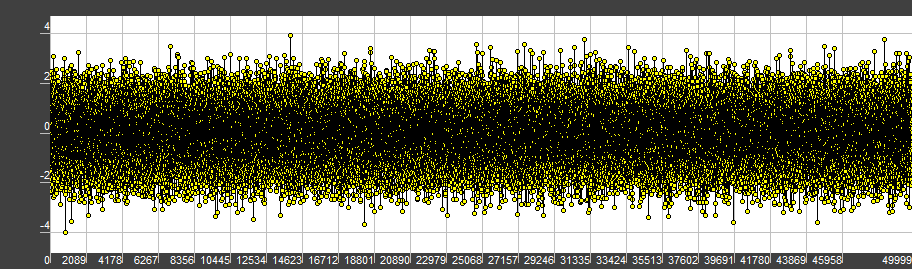
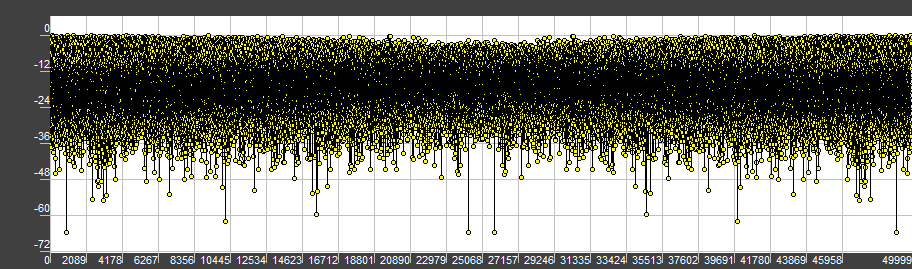
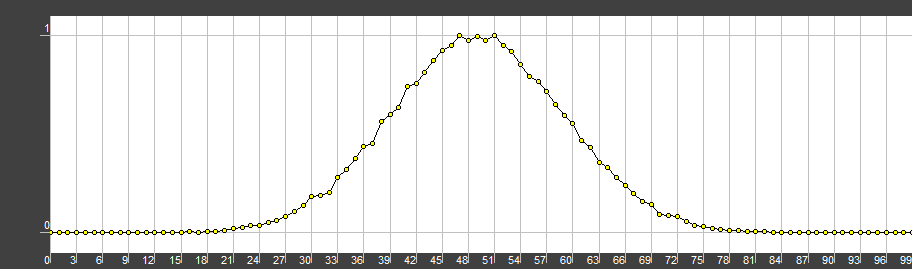
Now comes the interesting part, the normal distribution. During the runtime, I prefer to generate AWGN with the Box-Muller algorithm, because it’s simple, elegant and easy to understand (therefore, easy for the compiler to optimize). Unfortunately, current compilers have a very limited constexpr steps quantity and limited memory (did you know, that compilers never deallocate memory?). Due to the potentially long loop, we may run out of steps and memory quite soon, therefore, a small array of numbers.
This is the case, where the Irwin-Hall distribution may help us. \[\begin{aligned} X = \sum_{i=0}^n U_i \text{ for the } U = (U_1, U_2, ...) \end{aligned}\]
Irwin-Hall distribution is the sum of the n uniformly distributed values. Its probability density function may be represented as \[\begin{aligned} f_X(x;n)=\frac{1}{2(n-1)!}\sum_{k=0}^n (-1)^k{n \choose k} sign(x-k) (x-k)^{n-1} \end{aligned}\]
Generally speaking, one may not only sum the values, but also substract them. Most of the implementations I’ve came up with are limited to adding. Here’s the corresponding code:
template <typename T, std::size_t sz, std::size_t irwin_numbers = 12>
constexpr static auto normal_distribution(double mean, double sigma) {
std::array<T, sz> dst{};
auto previous = get_seed_constexpr();
for (auto &el : dst) {
double val = 0;
for (std::size_t i = 0; i < irwin_numbers; ++i)
val += uniform_distribution_n(previous);
// UPDATE: bug here. Should be std::sqrt((irwin_numbers / 12)),
// but std::sqrt is not constexpr by default,
// and I don't want to use any external libraries here by now
el = val / (irwin_numbers / 12) - irwin_numbers / 2;
}
return dst;
}
With this done we’ve managed to generate noise buffers at compile time, saving us the precious runtime. Was it worth it? It depends. If you’re working on some research, where you constantly have to rebuild your program, you will only waste time and numerous cups of coffee on debugging the constexpr compiler errors. Otherwise, if you’re shipping the application to many users, you may save a lot of time for them.
At the C++Russia conference in St. Petersburg this summer I had a very interesting talk with David Vandevoorde about constexpr and it’s future developments. According to David, constexpr will be more powerful and more forgiving in the next standard, there will be constexpr memory allocations, std::vector, constexpr! and many other things. This is a great idea and movement vector by any means, but I’m quite concerned about current constexpr state. Compilers have a very limited support for it, a small number of steps, compile-time operations take ages to finish, grab a whole lot of memory etc. I’m pretty sure, that the compiler vendors won’t be so happy about these changes, since it may require a ton of work on rewriting the constexpr engine. David has assured me, that as a compiler-guy himself, he’s looking forward to the upcoming standard and he really wants it to become real.