A tale about the pseudophase measurement drift and it's mitigation
During the development process of the MC149.01 GNSS receiver, we’ve got a delegation from the company making a reference station network. Their job is to make a Hydrogen Master clock-based station with three receivers inside. For one of their receivers they chose some of the Javad lineups, other two are vacant. Therefore, they came to us to test our device and, if all is good, include it in their master-device.
From the very beginning, I had some strange feeling about this. One of the delegation members wanted to know more about the system design and the frequency plan and tried to convince me that there is absolutely no way the receiver can work with an intermediate frequency of 12 MHz and it should be at least 100 MHz. Another claim was about our correlator interface, which by no means can be software-driven (registers) and should be LVDS and LVDS only. I’m sorry, I really had to pour this.
Anyway, we’ve agreed on them performing some tests of our receiver and giving us some feedback. It required some modifications on our side, like adding an external clock input (which is redundant in 99% of the applications) and forcing the post-processing software development.
Used method is quite simple:
- Collect long enough binary log files;
- Convert them to RINEX;
- Calculate and analyze the single differences
Since the receivers are connected to the same reference clock, their clock errors will cancel out. By single differencing the observations from the same satellite vehicles, we also mitigate the SV-based errors.
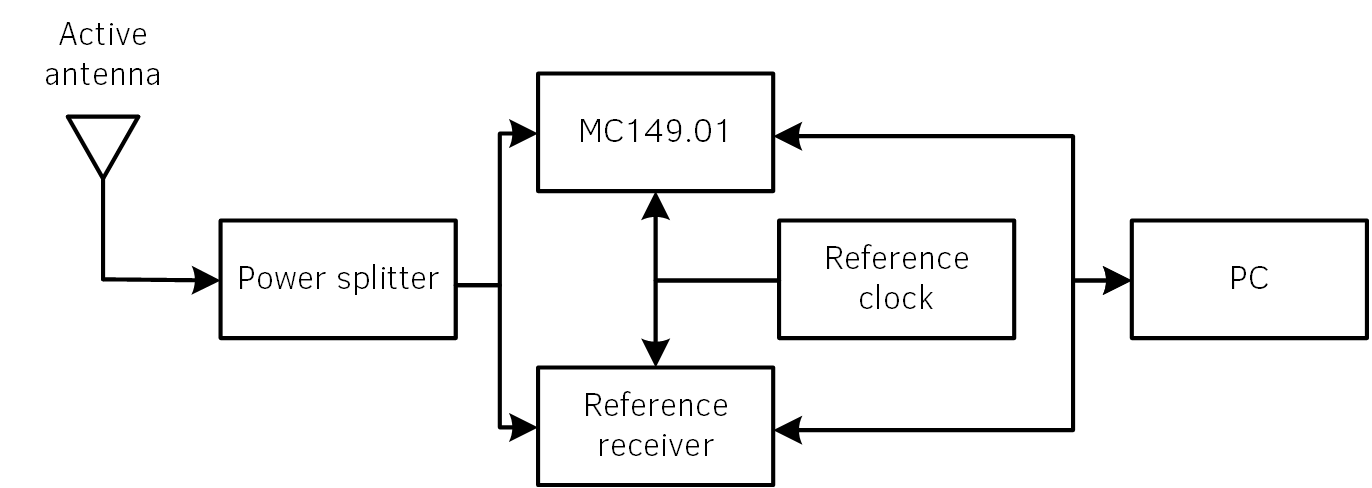
In this test scenario, our receiver was set with the Javad. One of the things pointed out by them was the enormous single difference phase drift.
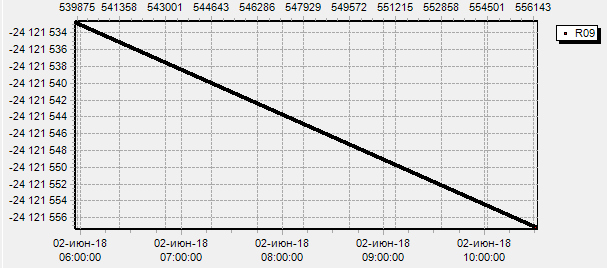
The funny thing is that it has absolutely zero influence on the RTK quality due to the double differencing, which will mitigate this drift among others hardware errors.
We had a couple of ideas, what could be the reason for such a phenomenon and we’ve decided to try a couple of things to mitigate it. One of the possible reasons is that we use two mixers in the digital domain: the first one translates the signal to the “zero” frequency, the second one in the correlator block is used to fine-translate the Doppler (and carrier frequency for GLONASS). Correlators’ heterodyne is being reset every 1ms epoch (starts with zero phase), so no error is being accumulated here. The first one in the DDC though is running continuously and has a rounding error due to the digital nature of the NCO: \[\begin{aligned} adder = f \cdot \frac{2^{32}}{F_s} = 14580000 \cdot \frac{2^{32}}{66500000} = 0x3820A512 \text{ for the GPS L1} \end{aligned}\]
This conversion has rounding error due to the integer arithmetics. With that adder we may restore the frequency: \[\begin{aligned} f_{restored} = adder \cdot \frac{F_s}{2^{32}} = 14579999.993788078427314758300781 \text{ Hz} \end{aligned}\]
And check the difference between the written and the real frequencies: \[\begin{aligned} abs(f_{restored} - f) = 0.006211921572685241699219 \text{ Hz} \end{aligned}\]
According to this calculations, there are an extra 0.006 cycles winding every second, which corresponds with the plot above. After I’ve zeroed the first NCO (with the corresponding fixes down the processing pipeline), we’ve managed to almost mitigate that drift.
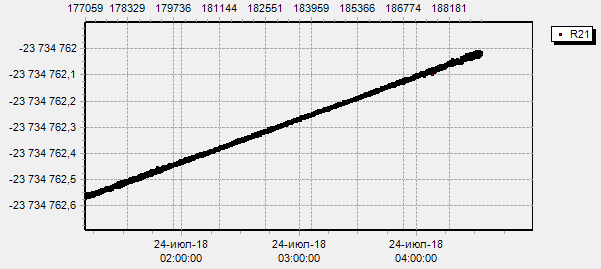
Now comes the interesting part. I’ve tested our receiver against Piksi Multi (report yet to be published, stay tuned) Javad and Trimble. Every single receiver has this phase drift when I’m calculating single differences, even the Trimble! Yet I can’t think of anyone saying that Trimble makes bad receivers. Therefore, this receiver comparison method results has nothing to do with the actual receiver accuracy.
To address this I’ve collected two zero-baseline logs from our MC149.01 receiver and processed them to get both standalone and RTK solutions. Both receivers are hardware-wise identical and only differ in firmware: one has this drift-compensation technique and the other hasn’t.
In terms of standalone, solutions are almost identical. This is not a surprise, because we’re not using any pseudorange smoothing methods.
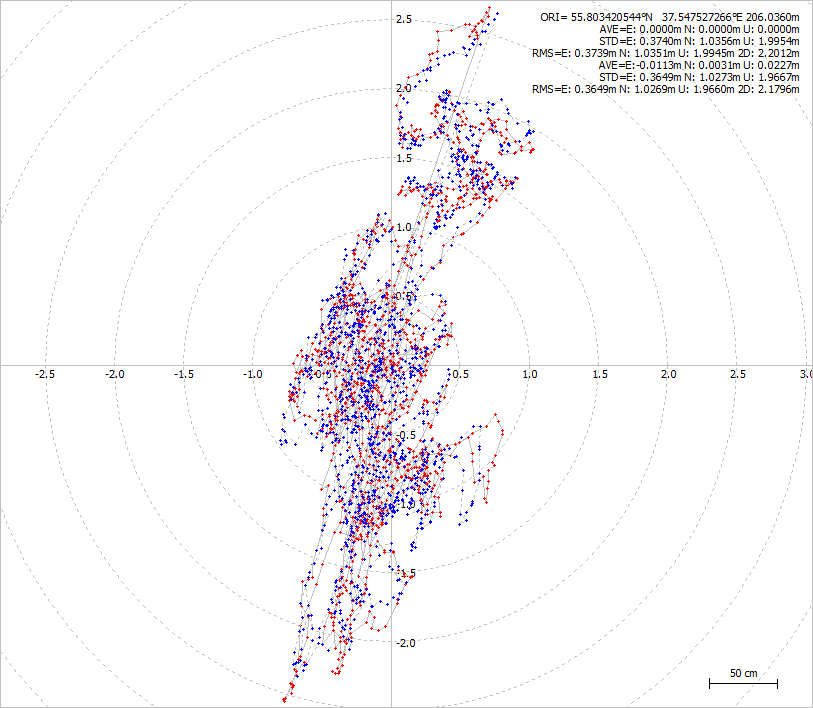
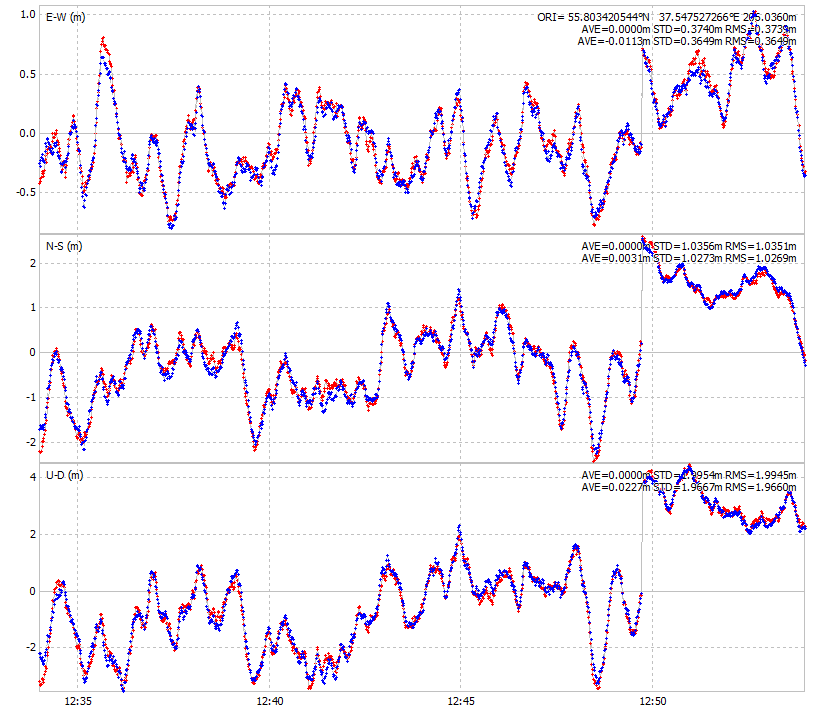
We’re more interested in the RTK solution, which heavily depends upon the pseudophase observations.
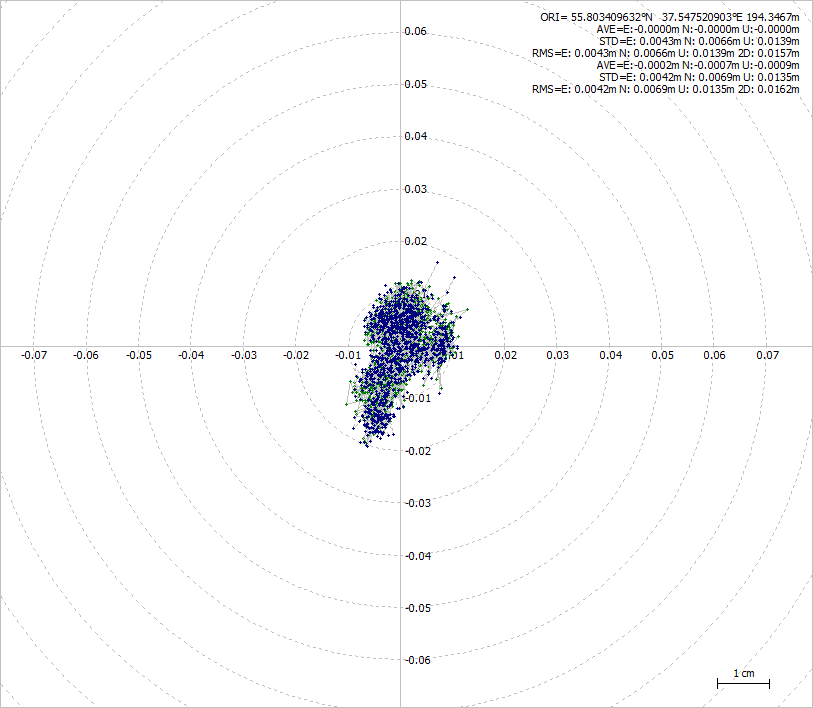
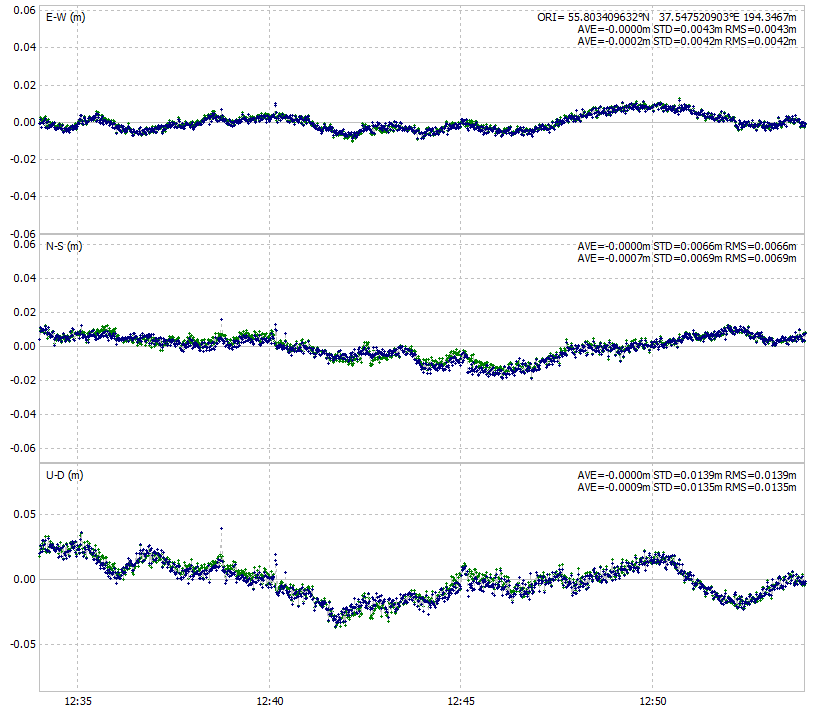
Once again, pretty identical. Therefore, this phase drift has nothing to do with the receiver’s quality.